コンプリート！ ヘロンの公式 例題 185881

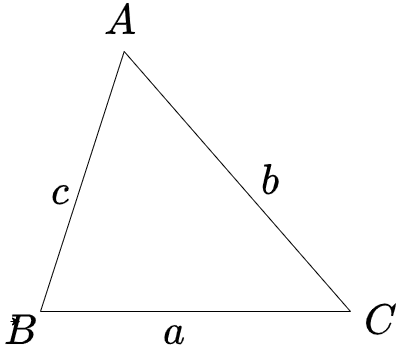
 ヘロンの公式 ヘロンの公式の使い方を、下の例題で確認してみましょう。 は , , である。 の面積 を求めよ。 ヘロンの公式を使うには、まず を求めましょう。 となります。 となります。 ヘロンの公式は常に効率的とは限らない。 とくに が分数に 3辺の長さから三角形の面積を求める公式です。 中学生から高校生まで、知っていると非常に便利な計算方法です。 ①ヘロンの公式と名前の由来 ②証明（中3レベル） ③証明（数Ⅰレベル） ①ヘロンの公式と名前の由来 ヘロンの公式 3辺の長さが $~a ,b,,c~$ の三角形がある。 ヘロンの公式 AB = c A B = c, BC = a B C = a, CA = b C A = b と書き、角の大きさは ∠CAB = A ∠ C A B = A, ∠ABC = B ∠ A B C = B, ∠BCA = C ∠ B C A = C と書くことにします。 標準三角比と三角形の面積 の例題のように、 a,b,c a, b, c がわかっているときに、この三角形の面積

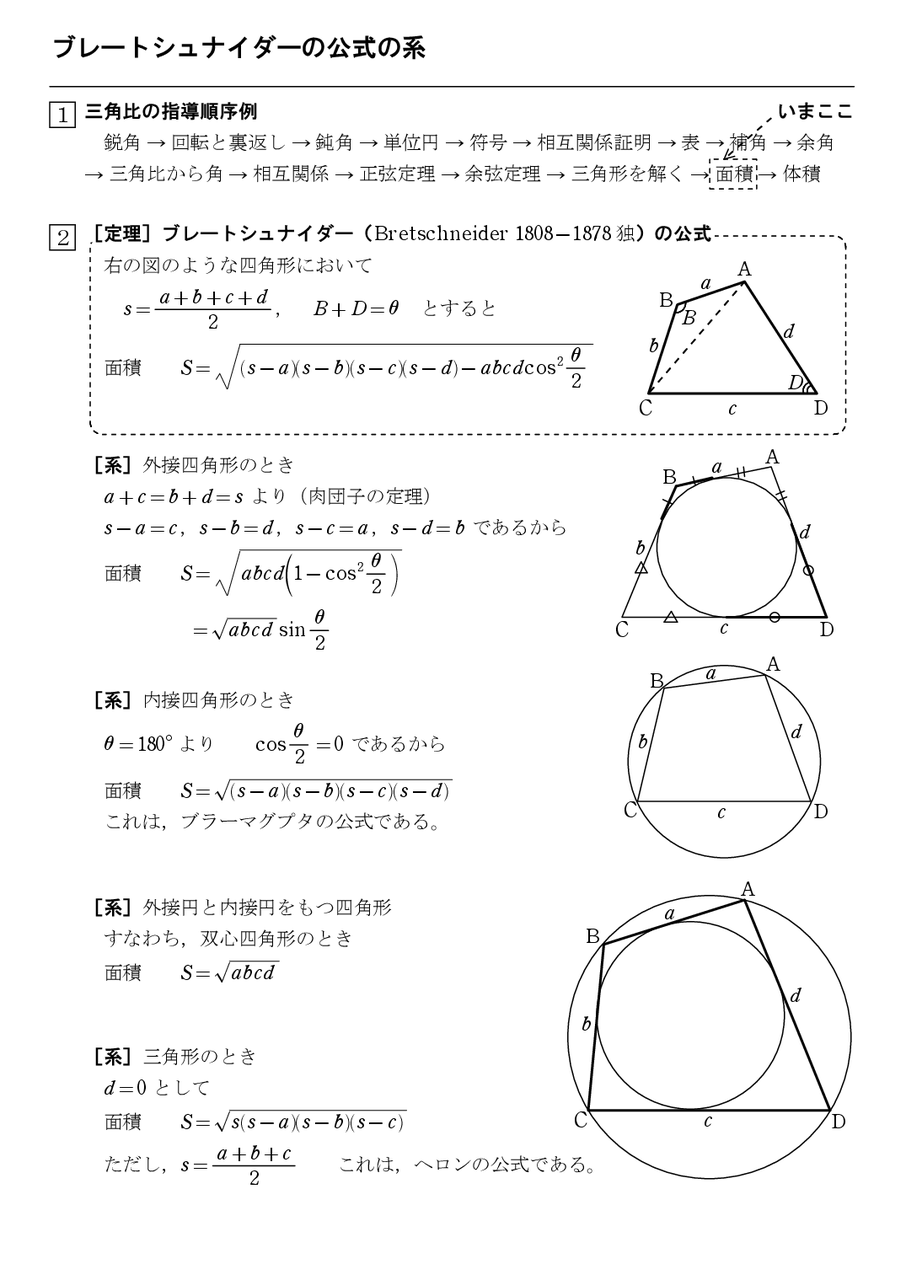
最高 ヘロン の 公式 証明 トップイラスト

ヘロンの公式 例題

ヘロンの公式 例題- ヘロンの公式 計算機が見つからず、手計算でやるかと思いましたが、検索してありました。 助かりました。 単一三角では便利ではありますが、通常舗装面積等は多くの三角形に集合体になります。 入力欄を増やす事は出来ませんでしょうか。 尚且つ数学1の教科書に載っている公式の解説一覧 まとめ 更新日時 数1の教科書（新課程）に載っている公式（や定義など）を整理しました。 リンク先ではその公式に関して踏み込んだ内容を解説しています。 は発展事項として教科書に載っている

６辺の長さから四面体の体積を求める例題 怜悧玲瓏 高校数学を天空から俯瞰する

Ⅲ ヘロンの公式を使う． 結論から言うと，Ⅱの 余弦定理 を使う方法が総合的に考えて1番メリットの多い方法です． ヘロンの公式は3辺が自然数のときしか使いにくい点と，覚え間違えリスクが大きいので，普通に数学の試験を受けるという点では不要だと例題 (12) 練習問題 練習問題＋解答 正弦定理 余弦定理 三角形の面積（ヘロンの公式） 三角比の値 練習プリント 三角比の値 練習プリント＋解答 AL教材三角形を解く三角形の決定条件 ヘロンの公式の証明 辺の長さが である2辺の間の角を とします。 三角比を用いた三角形の面積 より、 (1) 余弦定理 より、 (2) 三角比の相互関係式 より、 (3) (2)式を (3)式に代入する

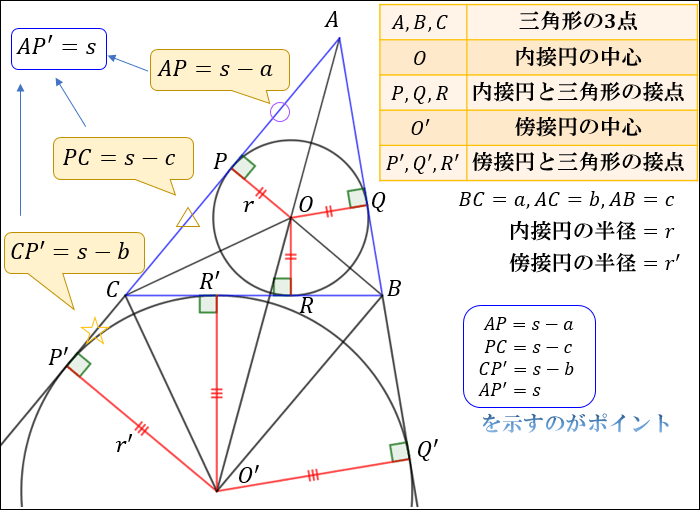
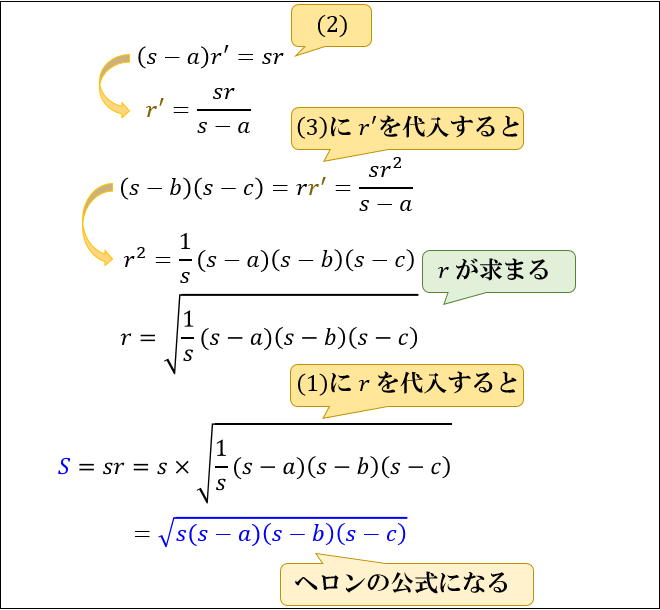
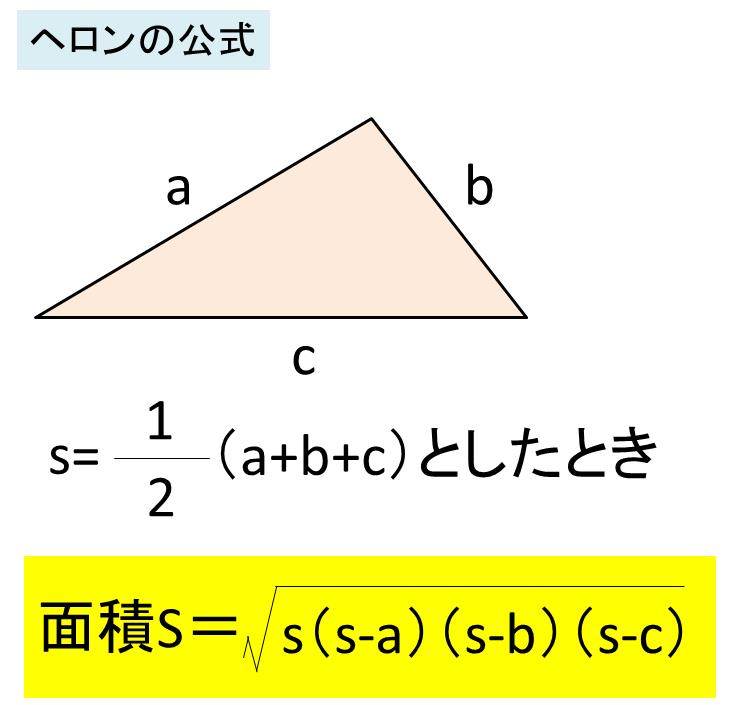
これまでの解説で ，三角比の図形への応用の講義はほぼ終わっているん だけれど，最後にもう1 つ，"ヘロンの公式"について教えよう 。 ヘロンの公式とは ， ABC の3 辺の長さ a，b，c が分かれば，これら ヘロンの公式の図解 Step① 内接円の性質から S = s r Step② s − a, s − b, s − c を見つける Step③ A P ′ = s を示す Step④ A P O と A P ′ O の相似 Step⑤ C O P と O ′ C P ′ の相似 Step⑥ (1), (2), (3) を解く 三角関数を用いた証明デジタル大辞泉 ヘロンの公式の用語解説 三角形の面積Sを3辺の長さa・b・cから求める公式。3辺の和の半分をsとすると、S2＝s（s−a）（s−b）（s−c）で与えられる。古代ギリシャの数学者・技術者ヘロン（Heron）によるが、ニュートンが再発見した。

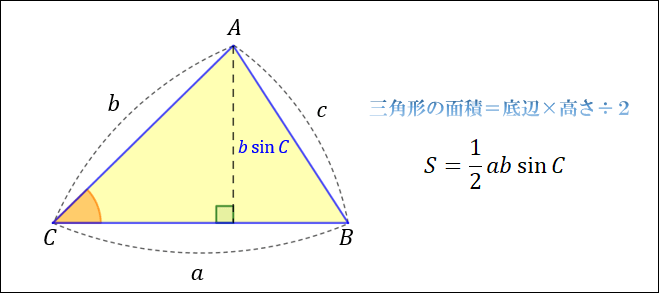
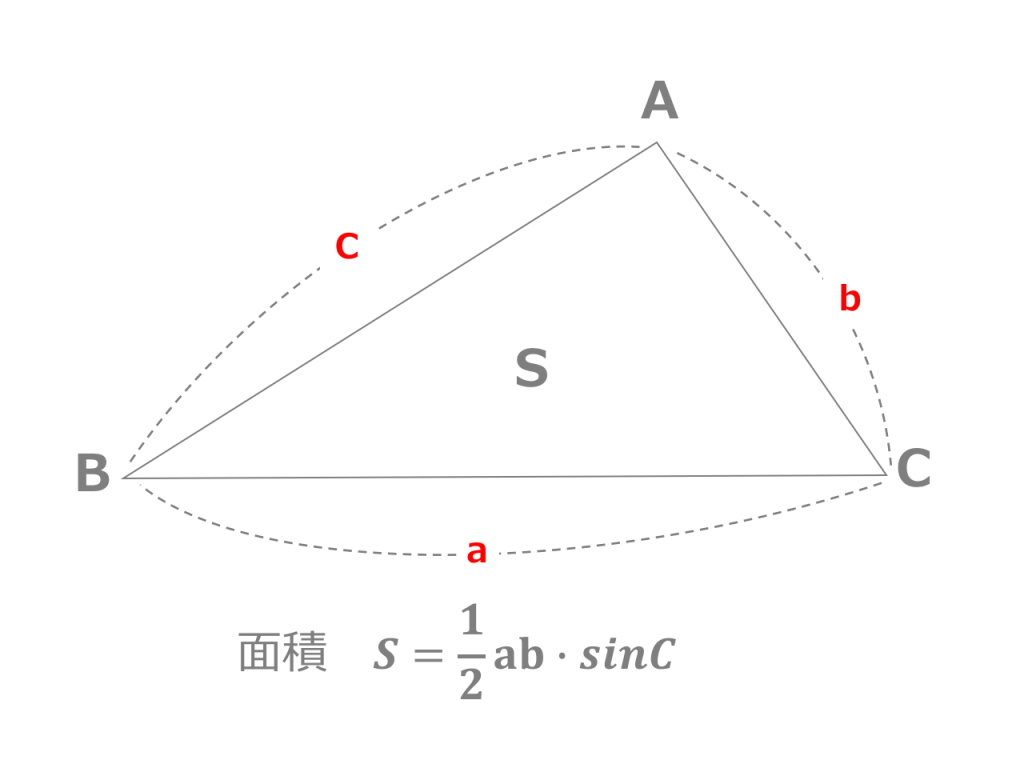
ヘロンの公式で求めた面積は、他の方法で求めた面積と等しいはずだということを使います。 例 三角形の3辺の長さが，それぞれ13,14,15のとき，内接円の半径を求めなさい （答案） s＝（）／2＝21 ヘロンの公式により、S＝ 他方，S＝21r ヘロン公式 三辺が分かっている場合の三角形の面積を求める公式になります。 S = s ( s − a) ( s − b) ( s − c) S=\sqrt {s (sa) (sb) (sc)} S = s(s − a)(s −b)(s − c) ※ s = a b c 2 s=\displaystyle\frac {abc} {2} s = 2a b cヘロンの公式を使わない場合は、 1 余弦定理でひとつの角の$\cos$を得る 2 $\sin^{2}\theta\cos^{2}\theta=1$を用いて、その角の$\sin$を得る 3 復習の2番目の公式を使って面積を求める という手順になる。 余弦定理より、

三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ

高校数学 数 ９４ 三角形の面積 ヘロンの公式編 Youtube

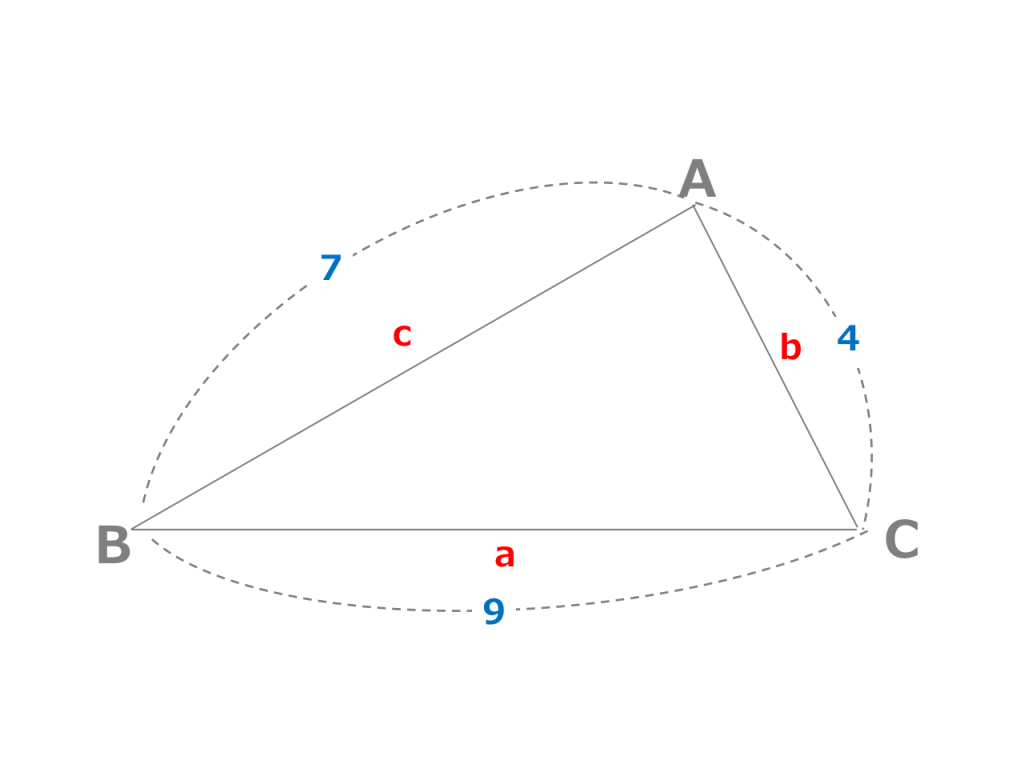
 （ヘロンの公式の証明の途中式（※）のルートの中身を整理することで得られます。 例題3 三辺の長さが 5 , 7 , 3 \sqrt{5},\sqrt{7},3 5 , 7 , 3 であるような三角形の面積を求めよ。ヘロンの公式の証明は → 例題16 ABC において，a=2,b=3,c=4 のとき，面積 S を求めよ。 解答 2s=234=9 とおくと，その面積 S は，ヘロンの公式より，公式を理解すれば、明日から測量の達人になれる かもしれません。 ①三角形の性質 ②単曲線 ③弦角弦長法（道路はクロソイド曲線、鉄道は3次曲線） ④縦断曲線 ⑤1／4法カーブ（土方カーブ） ⑥ヘロンの公式

四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト

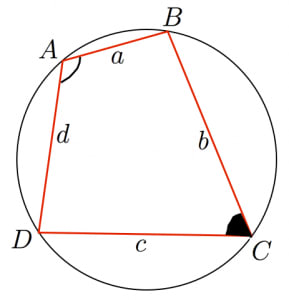
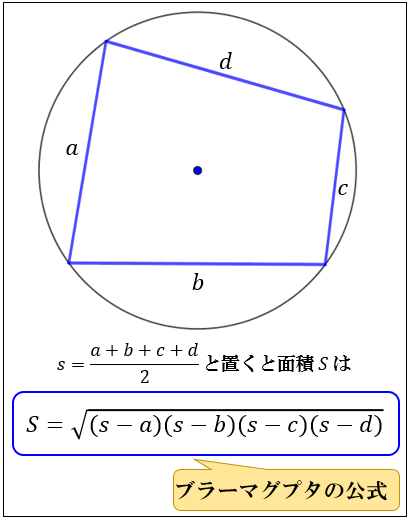
 例題3(ex3c) この例題は数学関数（sqrt()）を用いているので， TurtleEditを使わない（Linuxコマンドで操作する）場合には， コンパイルするときに（前回のヘロンの公式の計算プログラムと同様に）、 cc ex3c lm のようにccコマンドの最後に lm（スペース・ハイフン・エル・エム）オプションを偏微分と全微分 ここでは, 微分法 を学んだ人に向けてさらに踏み込んだ微分の概念, 偏微分 と 全微分 について紹介する 高校数学で登場する関数の多くは, 関数 f が1つの変数 x を指定することで値が定まる1変数関数 f = f ( x) であることが多かった しかし また、ブラーマグプタの公式において一辺の長さ \(d\) を \(0\) とするとヘロンの公式と一致しますね。 ブラーマグプタの公式の使い方例題 それでは、例題で実際に公式を使ってみま

ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト

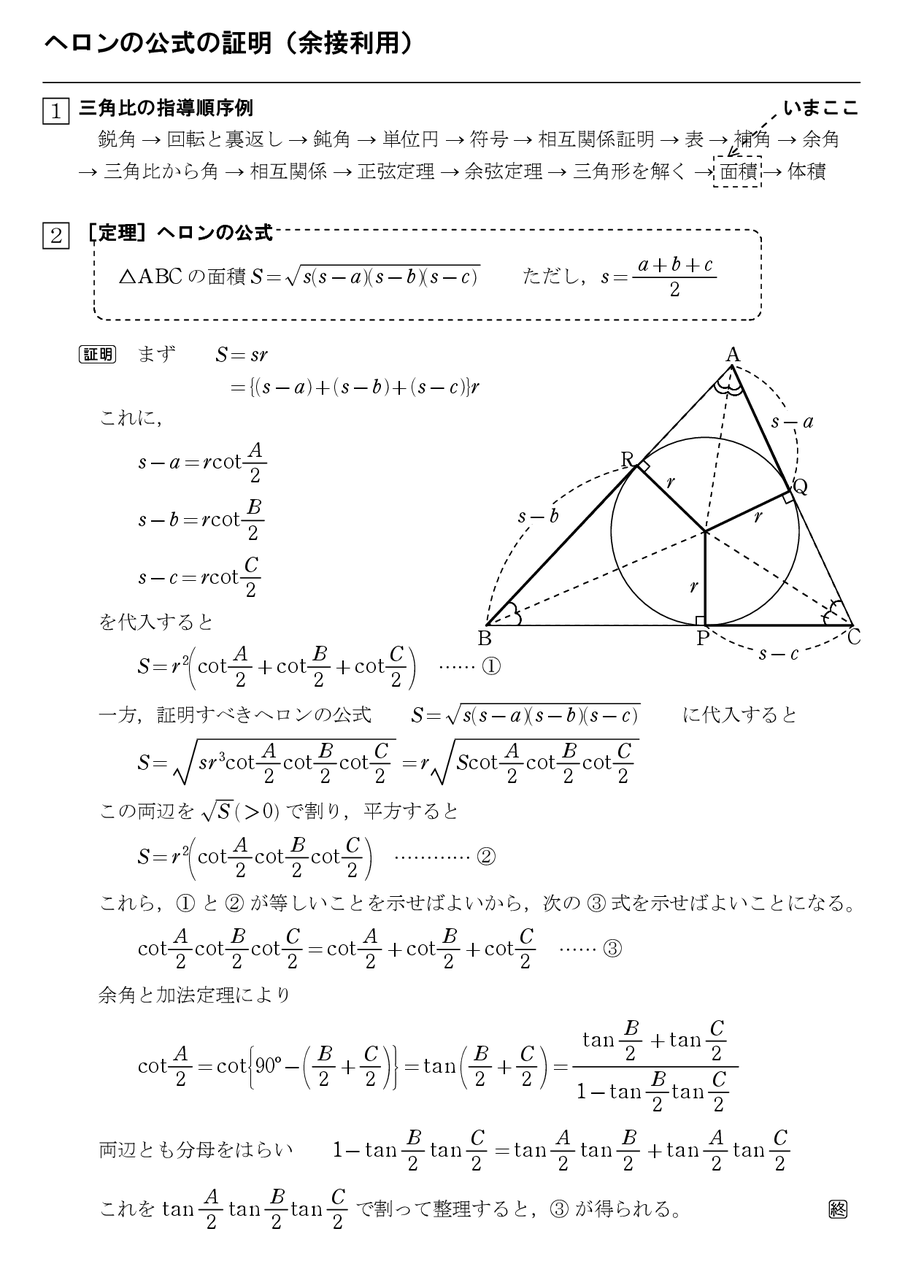
ヘロンの公式の証明 余接利用 怜悧玲瓏 高校数学を天空から俯瞰する

ヘロンの公式 計算機 説明！ ヘロンの公式を利用して、3辺の長さから三角形の面積を求めるプログラムです。 三角形の3辺の長さがそれぞれ a, b, c のとき、 とすると、三角形の面積Sは、 と表すことができる。 入力値は、整数・分数・小数のいずれか ヘロンの公式で解いてください 数学の問題です。Q次ような ABCの面積をヘロンの公式を利用して求めよa=5,b=6,c=7ヘロンの公式がいまいちわかりません詳しく解説していただけると嬉しいです。よろしくお願いします。 ヘロンの公式を用いる場合、まず三角形の3辺の長さの和の2分の1を求めます この記事ではこんなことを紹介しています 三角形の面積を求めるための公式の一つに"ヘロンの公式"というものがあります。 この公式はどんなときに使えるのでしょうか？ ここでは、ヘロンの公式が使える条件を説明したあと、実際に公式を使って三角形の面積を求める例題を示します。

ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト

1

辺長指定でヘロン・三斜図と面積表を入力するには 辺長指定でヘロン・三斜図と面積表を入力する操作例を解説します 。 P oint 4 向きを指定します。 （ 8 ） 5 隣接する3辺を連続で入力 する場合は残りの頂点を指 定して辺長を入力する操 作を繰り返し 中学数学で出来る！ ヘロンの公式の証明 21年2月3日 ヘロンの公式は、三角形の3辺の長さから面積を求める公式です 以下の三角形ABCの面積Sは S = s ( s − a) ( s − b) ( s − c) ( s = a b c 2) 今回は、この公式の「三角関数を使って証明する方法」と「中学ヘロンの公式とは ヘロンの公式とは、三角形の三辺の長さのみの情報からその面積を計算できる式のことを指します。 具体的には、 s＝1/2（abc）とした場合に、面積S＝（s（sa）（sb）（sc））^05 で表すことができる計算式がヘロンの公式です。

3分で分かる ヘロンの公式 証明と問題の解き方をわかりやすく 合格サプリ

ヘロンの公式で三角形の面積を求めよう パソコンカレッジ スタッフのひとりごと

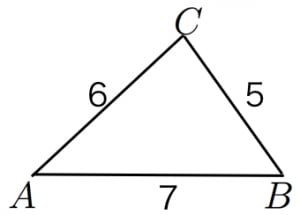
ヘロンの公式を思い出し手計算を行いこのサイトで確認してみました。 a=103 b=635 c=425 で3615程度になるはずが6315というおかしな計算結果になるのはなぜでしょうか ？ keisanより ヘロンの公式に当てはめると、 s=1045 になるので、 S=6312 となります。 目次 ヘロンの公式 例題 サンプルコード 実行結果 ヘロンの公式 三角形ABCについて、3辺の長さがわかれば、以下のように面積（S）を算出できる。 ただし、s（ルート内の小文字 s）は以下の通りである 例題 三ヘロンの公式を知っていても証明をしたことがないようなら，この問題には手も出なかったとなる かもしれませんね． 「ヘロンの公式は知っているけど， S = s ( s − a )( s − b )( s − c )の形しか習わなかった．」という声が聞こ

最高 ヘロン の 公式 証明 トップイラスト

ヘロンの公式 計算を工夫して証明 今週の定理 公式no 4 Youtube

Excel 測量計算（Ver2）は、様々な測量計算（30種）ができるように作られたソフトウェアです。 1,000点 の座標登録ができ、測点名で検索できます。 また、CSV や SIMAデータの作成、簡易図形表示もできます。 Excel 測量計算 Excel 測量計算：座標面積計算

ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ

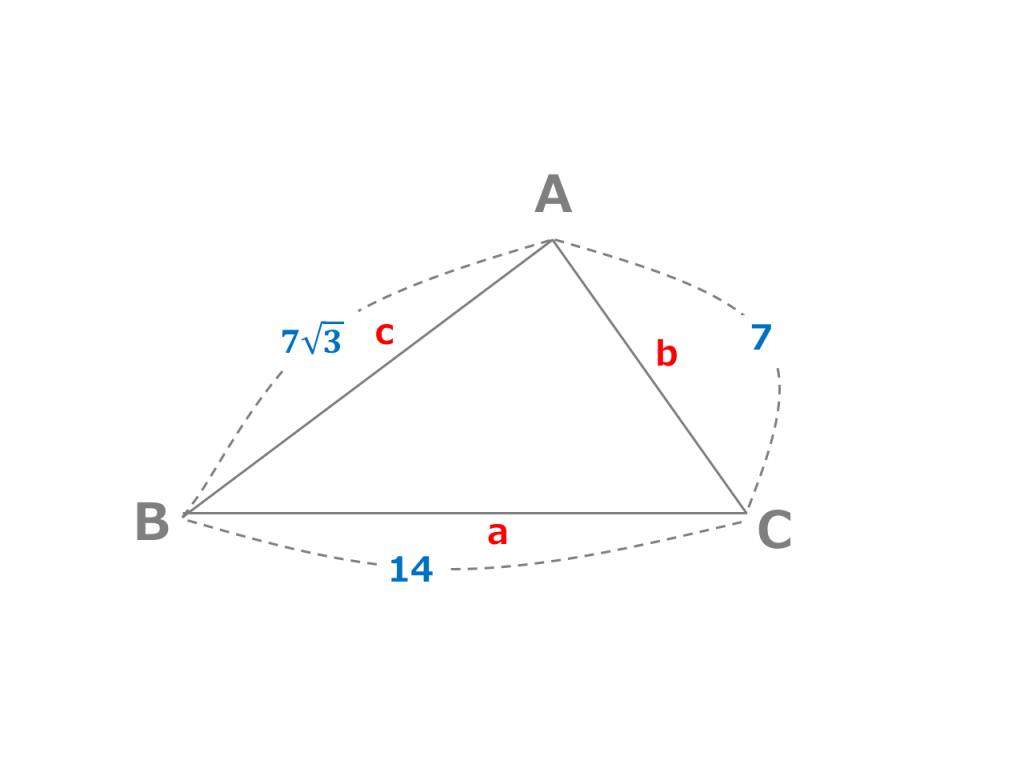
3分で分かる ヘロンの公式 証明と問題の解き方をわかりやすく 合格サプリ

Excel ヘロンの公式で三角形の面積を求める いきなり答える備忘録

ヘロンの公式 を使って面積を求める方法 証明あり ますますmathが好きになる 魔法の数学ノート

ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト

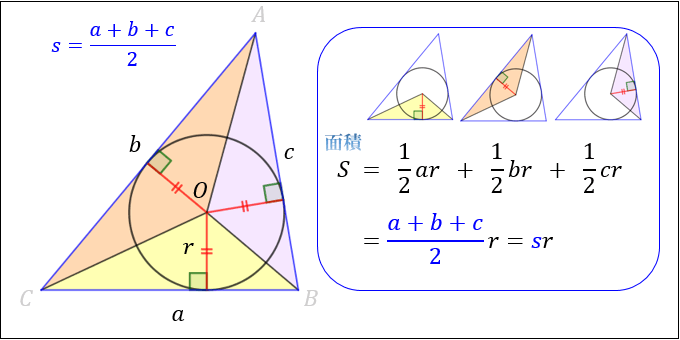
ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ

ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ

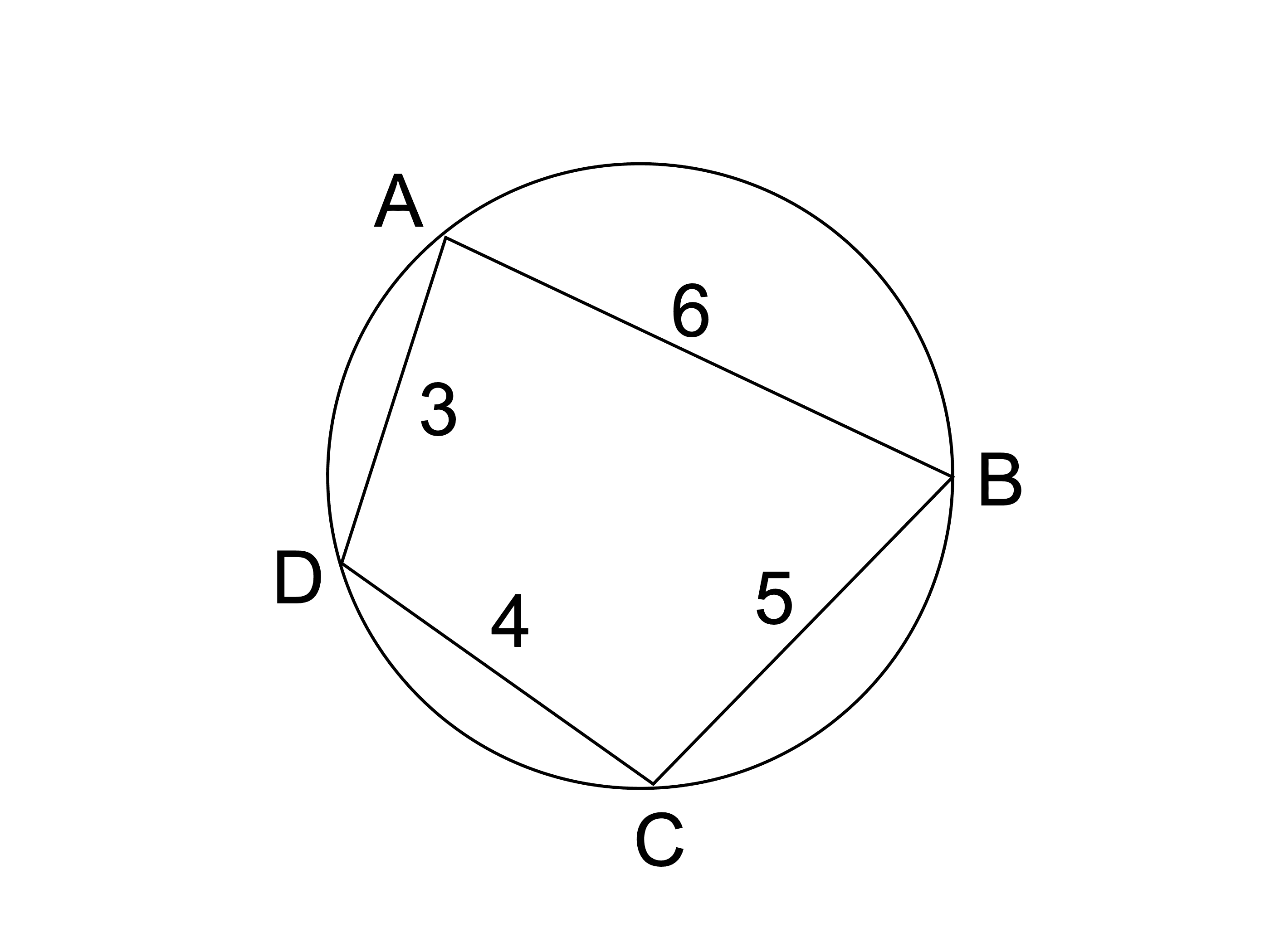
ブラーマグプタの公式とその２通りの証明 高校数学の美しい物語

ヘロンの噴水

ヘロンの公式 Wikipedia

内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ

ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ

ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する

高校数学でよく使う三角形の面積公式まとめ おいしい数学

高校数一 ヘロンの公式 を使いこなそう 三角形の面積の求め方のまとめ ジルのブログ

ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典

ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ

最高 ヘロン の 公式 証明 100以上の最高の絵のゲーム

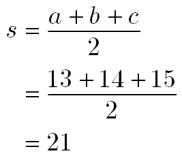
三角比 ヘロンの公式 の計算例 大人が学び直す数学

3分で理解 ヘロンの公式の使い方をイチからていねいに解説 数スタ

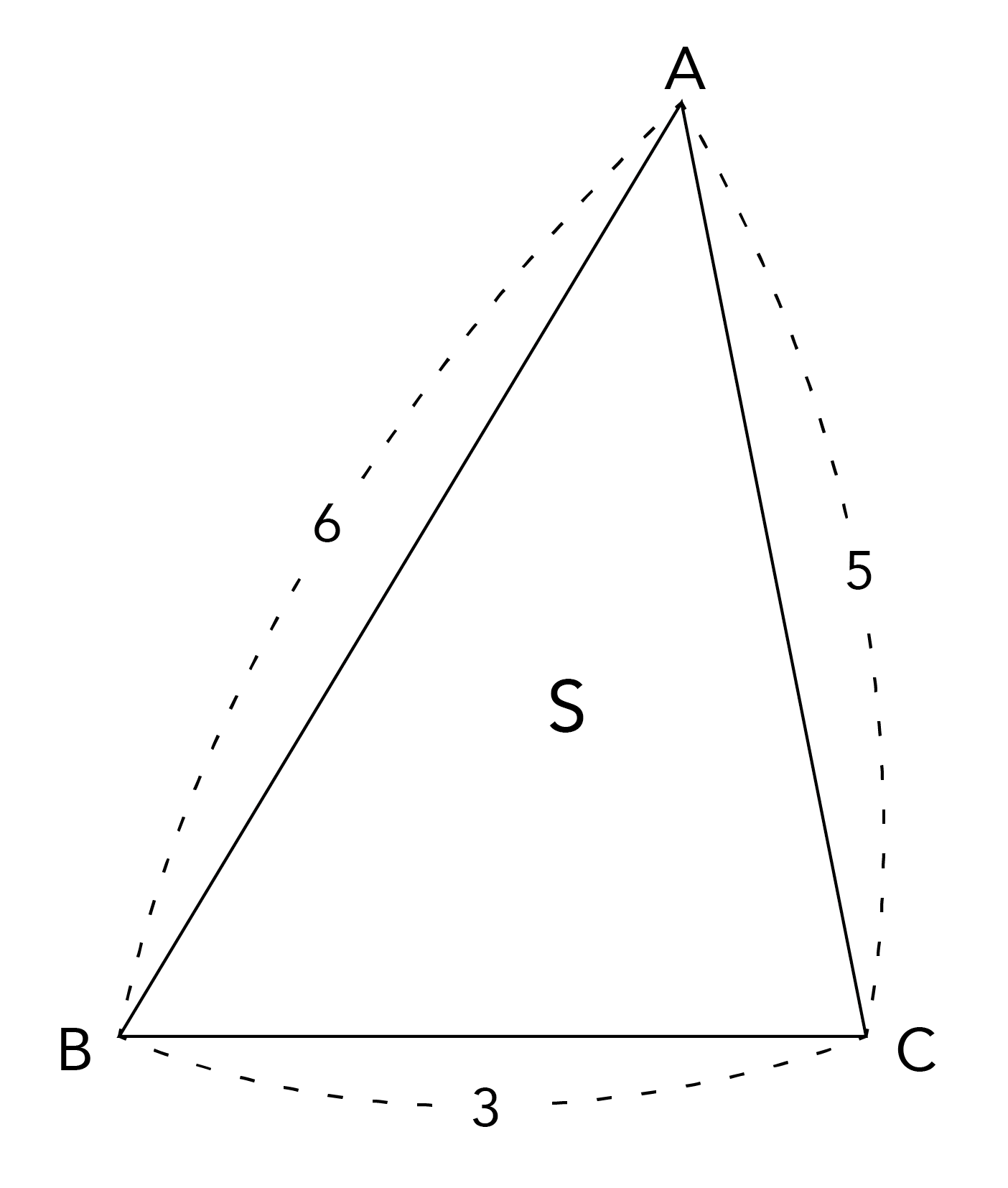
ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ

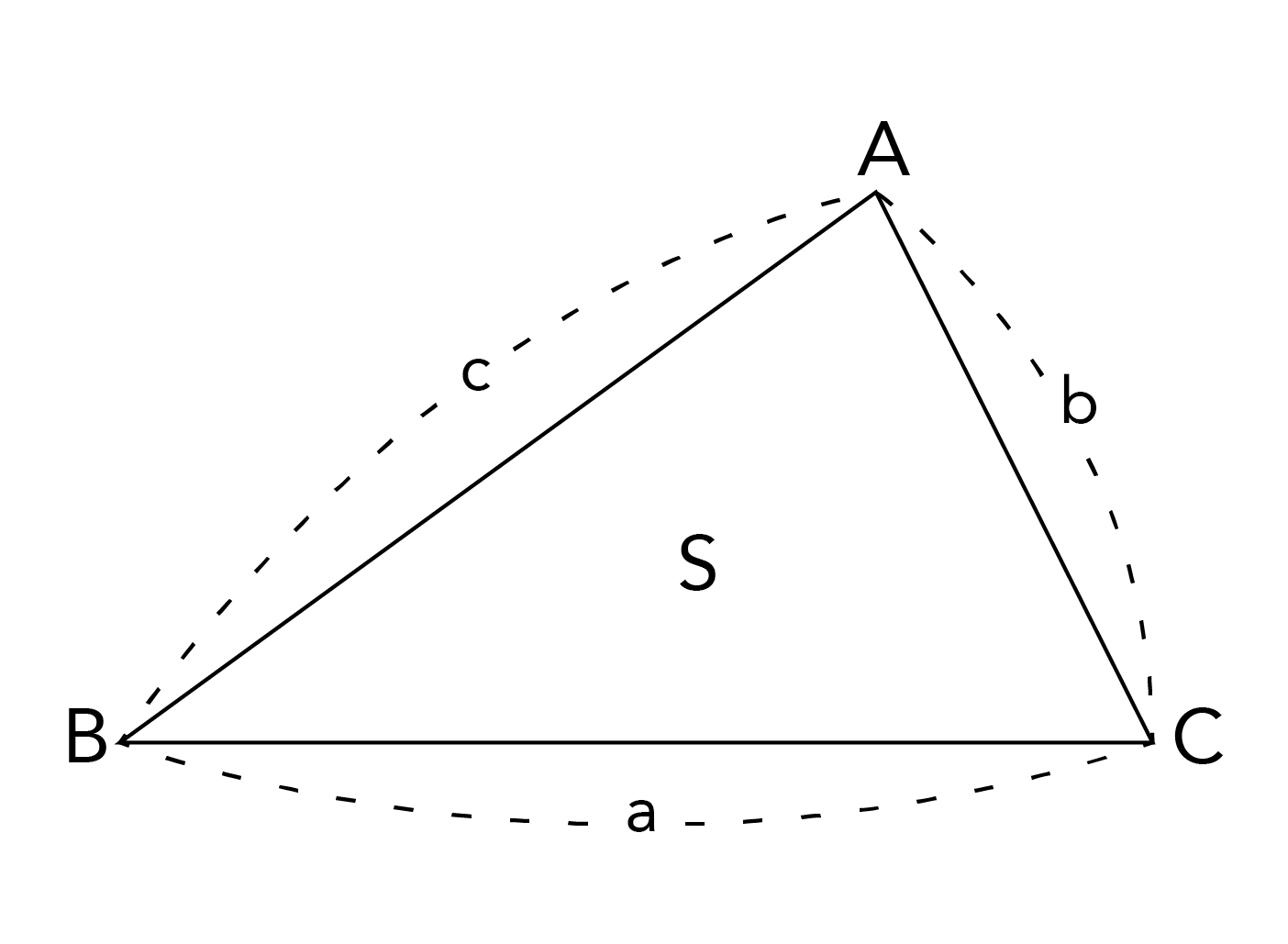
ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ

この数学の問題を ヘロンの公式を使わずに 三平方の定理での解き方を教え Yahoo 知恵袋

ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri

最高 ヘロン の 公式 証明 トップイラスト

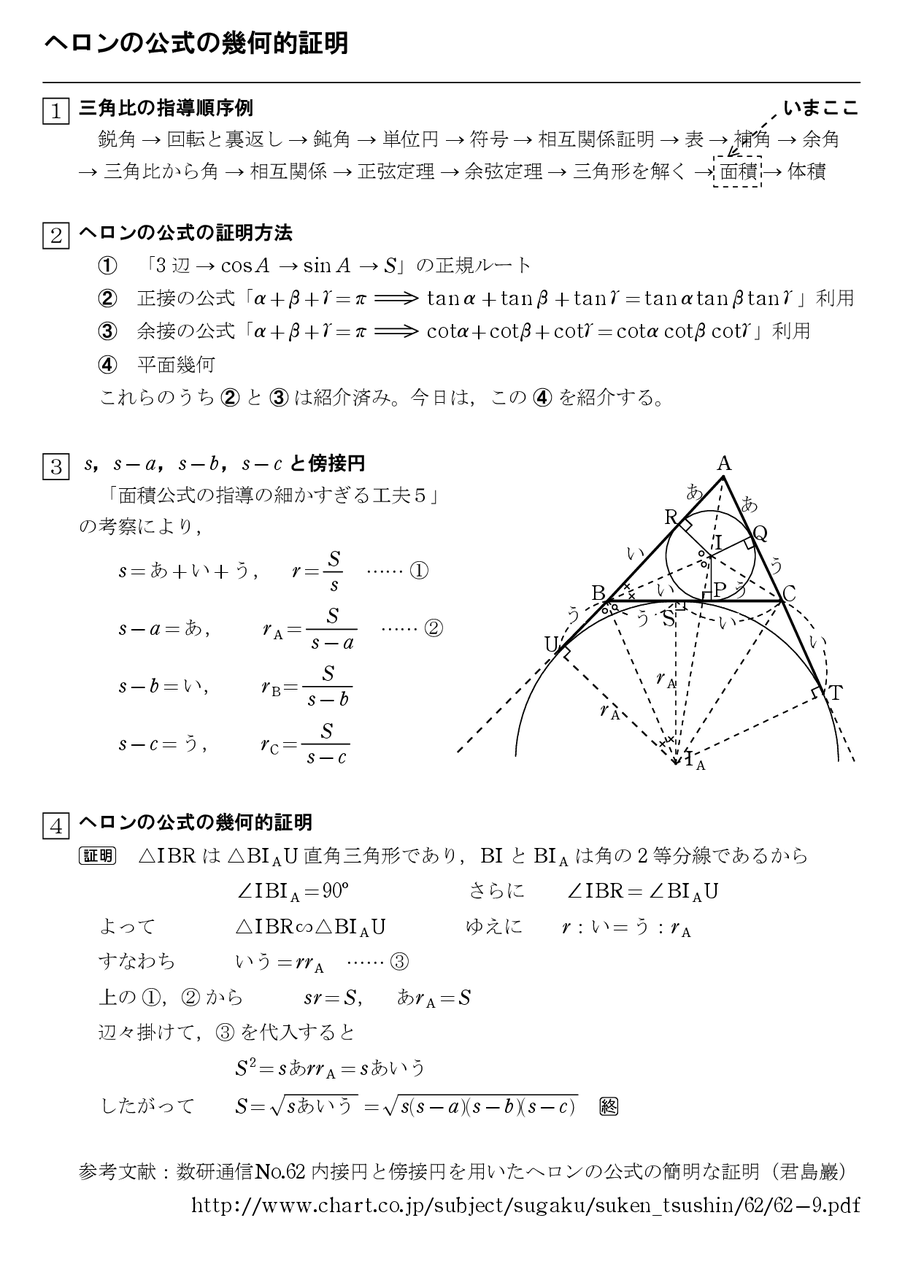
ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する

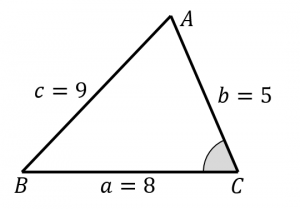
三角形の面積を３辺の長さから求める２つの方法 具体例で学ぶ数学

ヘロンの公式 その証明 身勝手な主張

高校数学 三角形の面積のヘロンの公式s S S A S B S C の証明と利用 受験の月

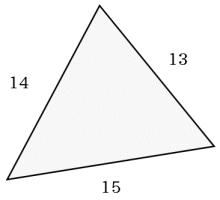
三角比 ヘロンの公式 の計算例 大人が学び直す数学

この数学の問題を ヘロンの公式を使わずに 三平方の定理での解き方を教え Yahoo 知恵袋

数学 チャート基本例題215 Clear

ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する

中学数学で出来る ヘロンの公式の証明

三辺の長さが与えられた三角形の面積を求めるヘロンの公式の別証明 身勝手な主張

ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典

Excel エクセルでヘロンの公式により三角形の面積を求める方法 計算

ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する

ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ

ヘロンの公式 東大合格コム

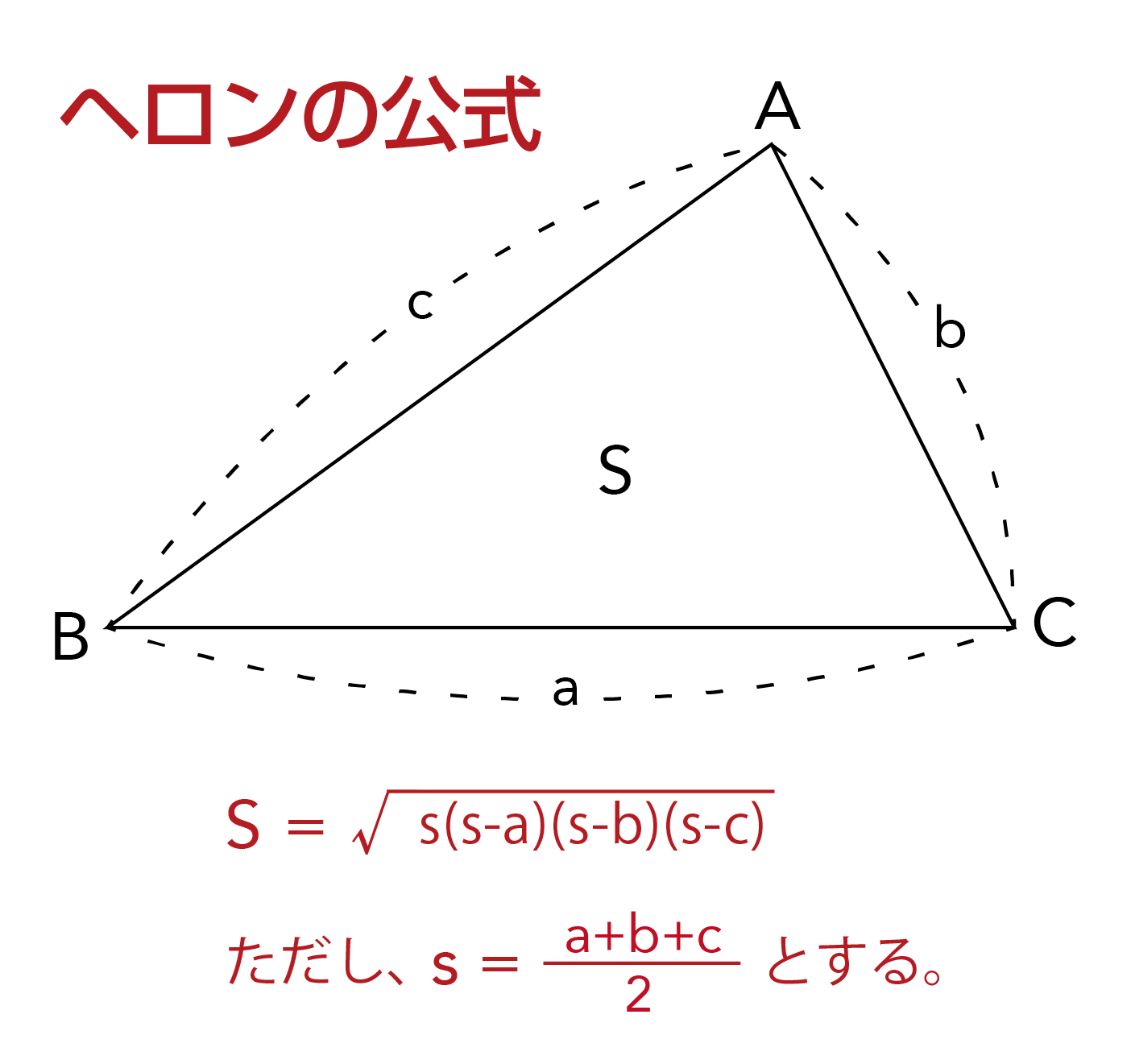
ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ

ヘロンの公式の証明と例題 数学i By ふぇるまー マナペディア

ヘロンの公式 思考力を鍛える数学

ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典

ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト

６辺の長さから四面体の体積を求める例題 怜悧玲瓏 高校数学を天空から俯瞰する

ヘロンの公式の証明と使用例 高校数学の美しい物語

面積公式の指導の細かすぎる工夫４ 怜悧玲瓏 高校数学を天空から俯瞰する

ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ

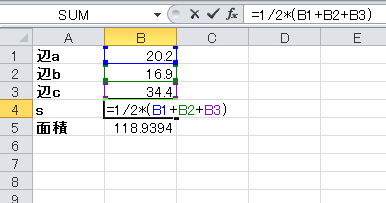
ヘロンの公式を用いて三角形の面積を求めるには Sqrtの解説 エクセル関数リファレンス

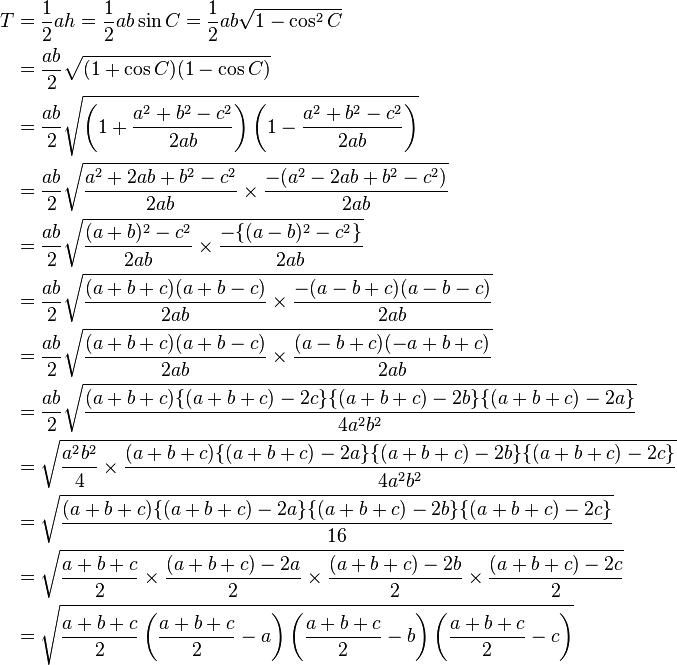
ヘロンの公式の証明 三角関数を使わずに ようこそ なるのホームページへ

中学 高校までの三角形の面積と面積比についてまとめました 高校生 Clearnote

ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト

ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト

ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する

5講 三角形の内接円と面積 3章 2節 三角形の応用 問題集 高校数学

最高 ヘロン の 公式 証明 トップイラスト

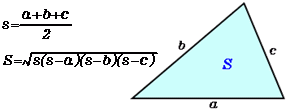
ヘロンの公式 高精度計算サイト

ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri

3分で分かる ヘロンの公式 証明と問題の解き方をわかりやすく 合格サプリ

ヘロンの公式の証明と使用例 高校数学の美しい物語

画像 ヘロンの公式 例題 ヘロンの公式 例題 Mbaheblogjpnqhd

ヘロンの公式 Wikipedia

数学 三角比 図形の計量 四平方の定理

ブラーマグプタの公式 17年 大阪教育大 数学日和

ヘロンの公式とは ヘロンノコウシキとは 単語記事 ニコニコ大百科

Python ヘロンの公式を使って三角形の面積を求める え のう

1

ヘロンの公式 Fukusukeの数学めも

ヘロンの公式 三角形の面積 大学入試数学の考え方と解法

画像 ヘロンの公式 例題 ヘロンの公式 例題 Mbaheblogjpnqhd

三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ

3分で分かる ヘロンの公式 証明と問題の解き方をわかりやすく 合格サプリ

高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト

ヘロンの公式 導出と計算例

3分で分かる ヘロンの公式 証明と問題の解き方をわかりやすく 合格サプリ

3辺の長さが与えられたときの三角形の面積 中学 高校数学 身勝手な主張

5講 三角形の内接円と面積 3章 2節 三角形の応用 問題集 高校数学

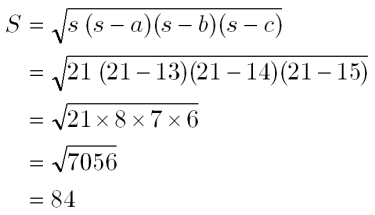
三角比 ヘロンの公式 の計算例 大人が学び直す数学

日暮里くん ヘロンの公式 三角形の3辺の長さから素早く面積を求める公式 オイラーの定理 内心と外心の距離を求める公式 T Co Ir01crbs61 Twitter

ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri

ヘロンの公式の証明と使用例 高校数学の美しい物語

3分で理解 ヘロンの公式の使い方をイチからていねいに解説 数スタ

5講 三角形の内接円と面積 3章 2節 三角形の応用 問題集 高校数学

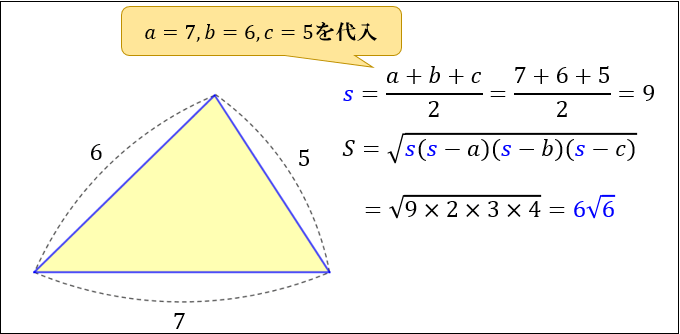
ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ

ちょっと中学 高校数学 ヘロンの公式とブラーマグプタの公式 Youtube

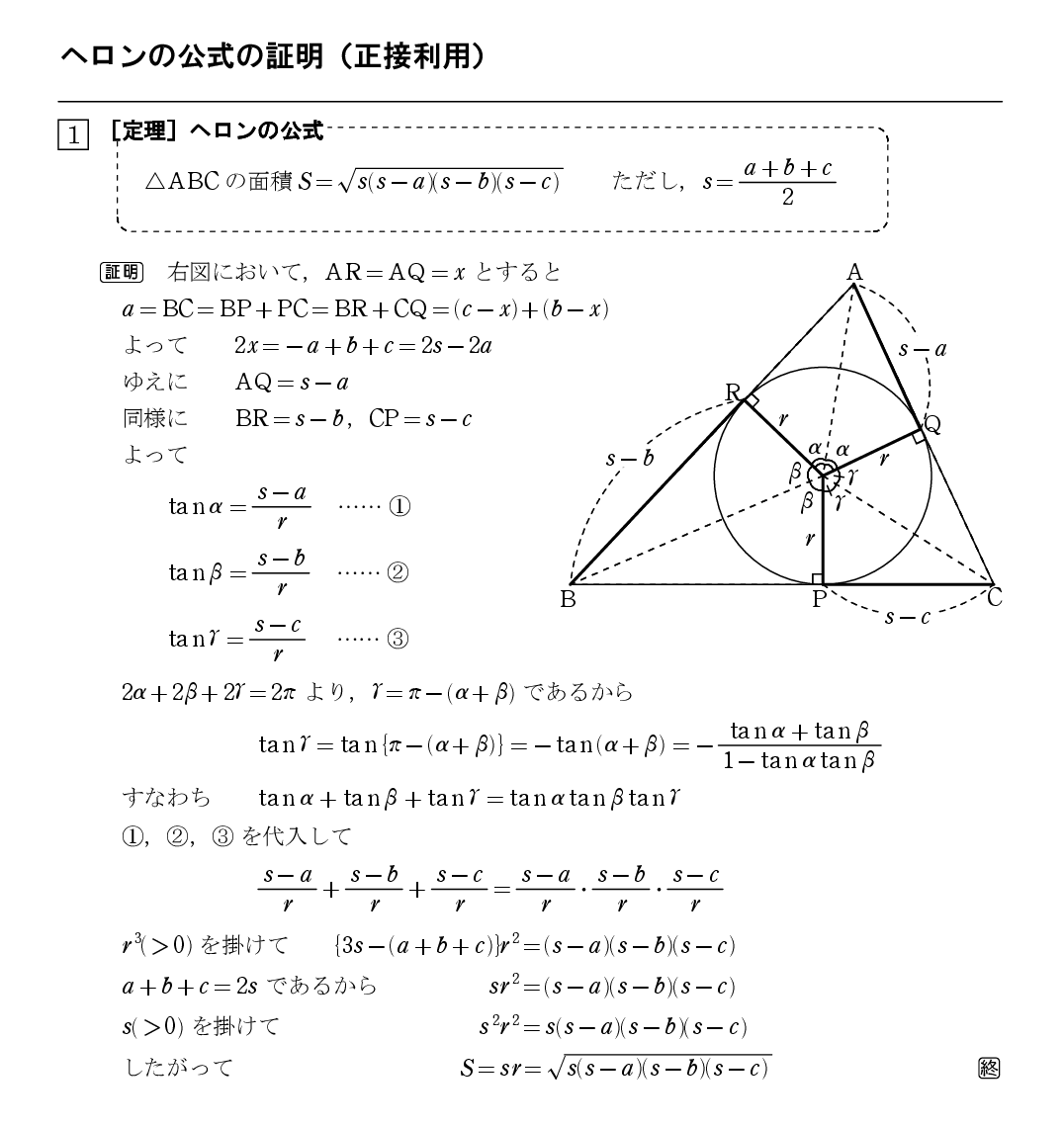
授業での雑談ネタ １８ ヘロンの公式の有名でない証明 怜悧玲瓏 高校数学を天空から俯瞰する

ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典

ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典

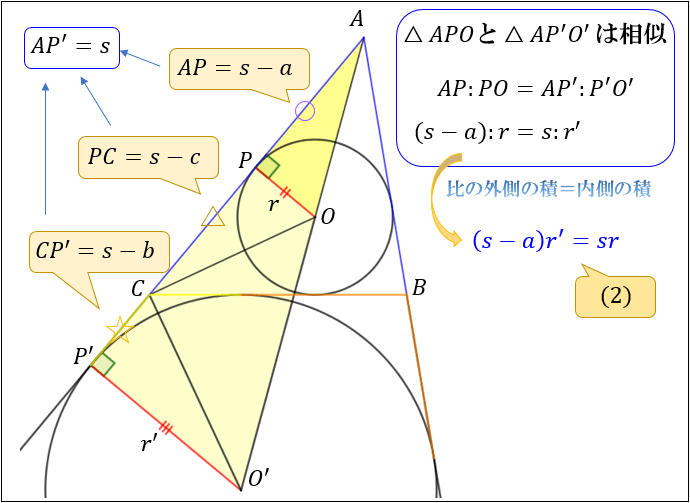
ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ

余弦定理

ヘロンの公式の証明 導出 を徹底解説 ５分でわかる Youtube